MTH304 Assignment 1 Solution and Discussion
-
Assignment # 1 MTH304 (Fall 2019)
Maximum Marks: 20
Due Date: 17 -11-2019DON’T MISS THESE: Important instructions before attempting the solution of this assignment:
• To solve this assignment, you should have good command over First 10 lectures.• Try to get the concepts, consolidate your concepts and ideas from these questions which you learned in first 10 lectures.
• Upload assignments properly through LMS, No Assignment will be accepted through email.
• Write your ID on the top of your solution file.
• Don’t use colorful back grounds in your solution files.
• Use Math Type or Equation Editor etc for mathematical symbols.
• You should remember that if we found the solution files of some students are same then we will reward zero marks to all those students.
• Try to make solution by yourself and protect your work from other students, otherwise you and the student who send same solution file as you will be given zero marks.
• Also remember that you are supposed to submit your assignment in Word format any other like scan images etc will not be accepted and we will give zero marks correspond to these assignments.Question No. 1:
A particle of mass 10kg is placed on an inclined plane which makes and angle of with the horizontal. Find the resolved parts of the weight of the particle in the direction parallel and perpendicular to the plane. MARKS 10
Question No. 2:
Two particles of mass 3kg each are connected by a light inextensible string which passes over a smooth fixed pulley, which is attached to a string C. The string C is hanging on the fixed support. The particles are at rest. Find the tension in the string C. MARKS 10
-
Solution of Assignment # 1 MTH304 (Fall 2019)
Maximum Marks: 20
Due Date: 17 -11-2019Question No. 1:
A particle of mass 10kg is placed on an inclined plane which makes and angle of with the horizontal. Find the resolved parts of the weight of the particle in the direction parallel and perpendicular to the plane. MARKS 10
Solution

Question No. 2:
Two particles of mass 3kg each are connected by a light inextensible string which passes over a smooth fixed pulley, which is attached to a string C. The string C is hanging on the fixed support. The particles are at rest. Find the tension in the string C. MARKS 10
Solution

-
@zareen said in MTH304 Assignment 1 Solution and Discussion:
A particle of mass 10kg is placed on an inclined plane which makes and angle of with the horizontal. Find the resolved parts of the weight of the particle in the direction parallel and perpendicular to the plane. MARKS 10
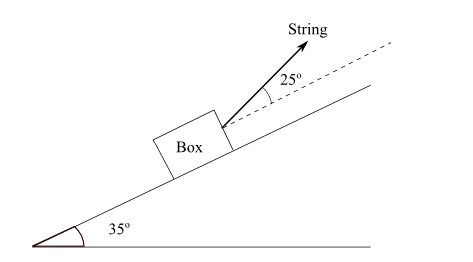
Free Body Diagram
T tension of string, W weight of the box, N force normal to and exerted by the inclined plane on the box, Fs is the force of frictionForces and their components on the x-y system of axis.
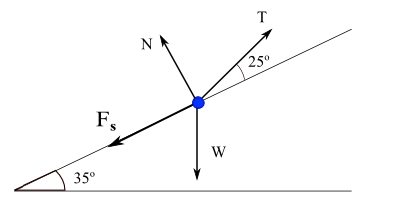
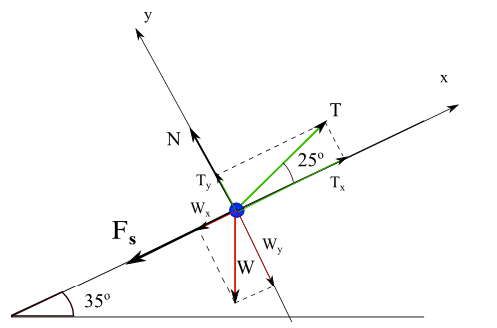
Equilibrium: W + T + N + Fs = 0
Forces represented by their components
W = (Wx , Wy) = ( - M g sin(35°) , - M g cos(35°))
T = (Tx , Ty) = (|T| cos (25°) , |T| sin (25°) )
N = (0 , Ny) = (0 , |N|)
Fs = (- |Fs| , 0) = ( - μs |N| , 0) , where μs is the coefficient of friction between the box and the inclined plane.
Sum of x components = 0- M g sin(35°) + |T| cos (25°) + 0 - μs |N| = 0
which may be rewritten as
|T| cos (25°) = μs |N| + M g sin(35°)
sum of y components = 0- M g cos(35°) + |T| sin (25°) + |N| + 0 = 0
|T| sin (25°) = M g cos(35°) - |N|
We now need to solve the system of two equations with two unknowns |T| and |N|.
|T| cos (25°) = μs |N| + M g sin(35°) (equation 1)
|T| sin (25°) = M g cos(35°) - |N| (equation 2)
solve equation 2 above for |N| to get
|N| = M g cos(35°) - |T| sin (25°)
Substitute |N| by M g cos(35°) - |T| sin (25°) in eq 1 to get
|T| cos (25°) = μs [ M g cos(35°) - |T| sin (25°) ] + M g sin(35°)
rewrite above equation as follows
|T| [ cos (25°) + μs sin (25°) ] = μs M g cos(35°) + M g sin(35°)
Solve for |T|
|T| =
- M g cos(35°) + |T| sin (25°) + |N| + 0 = 0
μs M g cos(35°) + M g sin(35°)
cos (25°) + μs sin (25°)
Substitute with numerical Values
μs = 0.3, M = 10 Kg, g = 10 m/s^2
|T| ≈ 79.3 NUse |N| = M g cos(35°) - |T| sin (25°) found above
|N| = 100 cos(35°) - 79.3 sin (25°) ≈ 48.4 N - M g sin(35°) + |T| cos (25°) + 0 - μs |N| = 0
-
@zareen said in MTH304 Assignment 1 Solution and Discussion:
Two particles of mass 3kg each are connected by a light inextensible string which passes over a smooth fixed pulley, which is attached to a string C. The string C is hanging on the fixed support. The particles are at rest. Find the tension in the string C.

Replace 6 with 3
-
Solution of Assignment # 1 MTH304 (Fall 2019)
Maximum Marks: 20
Due Date: 17 -11-2019Question No. 1:
A particle of mass 10kg is placed on an inclined plane which makes and angle of with the horizontal. Find the resolved parts of the weight of the particle in the direction parallel and perpendicular to the plane. MARKS 10
Solution

Question No. 2:
Two particles of mass 3kg each are connected by a light inextensible string which passes over a smooth fixed pulley, which is attached to a string C. The string C is hanging on the fixed support. The particles are at rest. Find the tension in the string C. MARKS 10
Solution
