STA631 Assignment 1 Solution and Discussion
-
Assignment No.1 (Course STA 631)
Fall 2019 (Total Marks 20)Deadline
Your Assignment must be uploaded/ submitted before or on November 14, 2019, Time 23:59
(STUDENTS ARE STRICTLY DIRECTED TO SUBMIT THEIR ASSIGNMENT BEFORE OR BY DUE DATE. NO ASSIGNMNENT AFTER DUE DATE WILL BE ACCEPTED VIA E.MAIL).
Rules for Marking
It should be clear that your Assignment will not get any credit IF:
• The Assignment submitted, via email, after due date.
• The submitted Assignment is not found as MS Word document file.
• There will be unnecessary, extra or irrelevant material.
• The Statistical notations/symbols are not well-written i.e., without using MathType software.
• The Assignment will be copied from handouts, internet or from any other student’s file. Copied material (from handouts, any book or by any website) will be awarded ZERO MARKS. It is PLAGIARISM and an Academic Crime.
• The medium of the course is English. Assignment in Urdu or Roman languages will not be accepted.
• Assignment means Comprehensive yet precise accurate details about the given topic quoting different sources (books/articles/websites etc.). Do not rely only on handouts. You can take data/information from different authentic sources (like books, magazines, website etc.) BUT express/organize all the collected material in YOUR OWN WORDS. Only then you will get good marks.Objective(s) of this Assignment:
The assignment is being uploaded to build up the concepts of Inferential statistics.
Assignment # 01 (Lessons 1-9)
Question 1: Marks: 10
Suppose are iid with pdf zero elsewhere. Find the MLE of
Question 2: Marks: 10
Let X be a Bernoulli . Thus the pdf of Bernoulli distribution is
Find the Fisher Information -
@zareen said in STA631 Assignment 1 Solution and Discussion:
Suppose are iid with pdf zero elsewhere. Find the MLE of
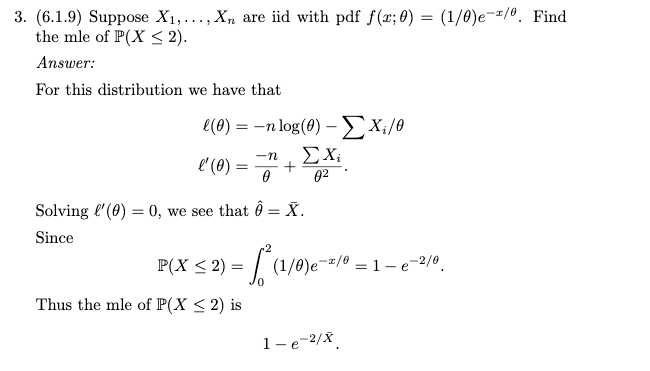
-
@zareen said in STA631 Assignment 1 Solution and Discussion:
Let X be a Bernoulli . Thus the pdf of Bernoulli distribution is
-
@zareen said in STA631 Assignment 1 Solution and Discussion:
Suppose are iid with pdf zero elsewhere. Find the MLE of
@zareen
3. (6.1.9) SupposeX1,…,Xnare iid with pdff(x;θ) = (1/θ)e−x/θ. Findthe mle ofP(X≤2).Answer:For this distribution we have that(θ) =−nlog(θ)−∑Xi/θ′(θ) =−nθ+∑Xiθ2.Solving`′(θ) = 0, we see thatˆθ= ̄X.SinceP(X≤2) =∫20(1/θ)e−x/θ= 1−e−2/θ.Thus the mle ofP(X≤2) is1−e−2/ ̄X. -
sta631 Assignment 1 solution 2023
-
@fatima-batool
please post assignment

