CS502 Assignment No. 01 Solution and Discussion
-
-
-
-
-
Solution:
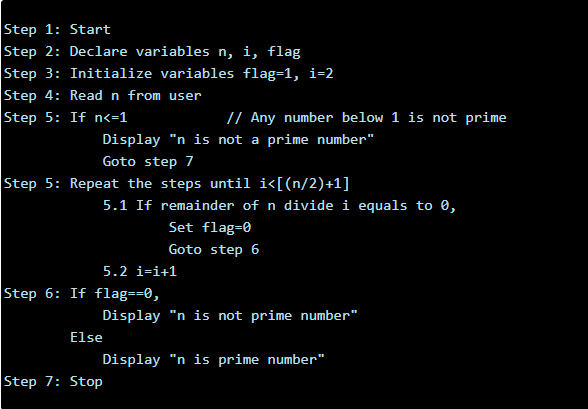
Question No. 01: The algorithm for the identification of Prime number is as follows,1 PRIME (int Number)
2 int Count ← 0
3 for i ← 2 to Number – 1
4 if ( Number % i equal to 0)
5 Increment Count
6 If (Count is equal to 0)
7 Number is Prime
8 else
9 Number is NOT Prime -
Question No. 02: The step by stem analysis of the algorithm designed in question 1 is as follow,
The time taken by each statement (step) is given as follows,
Step 1: C1 // Execute only 1 time or Constant Time or O (1)
Step 2: C2 // Execute only 1 time or Constant Time or O (1)
Step 3: n -2 // Execute n -2 times
Step 4: n -2 // Execute n -2 times
Step 5: n – 2 // Execute n -2 times
Step 6: C3 // Execute only 1 time or Constant Time or O (1)
Step 7: C4 // Execute only 1 time or Constant Time or O (1)
Step 8: C5 // Execute only 1 time or Constant Time or O (1)
Step 9: C6 // Execute only 1 time or Constant Time or O (1)Total time T(n) can be calculated as follows,
T(n) = C1 + C2 + (n -2 ) + (n -2 ) + (n -2 ) + C3 + C4 + C5 + C6
T(n) = C1 + C2 + n -2 + n -2 + n -2 + C3 + C4 + C5 + C6
T(n) = C1 + C2 + n + n + n - 6 + C3 + C4 + C5 + C6
T(n) = 3n + C1 + C2 + C3 + C4 + C5 + C6 -6
T(n) = 3n + (C1 + C2 + C3 + C4 + C5 + C6 -6)
T(n) = 3n + C7 // C7 = (C1 + C2 + C3 + C4 + C5 + C6 -6)
T(n) = n // Ignoring constant termsOr T(n) = O (n )
-
@zareen said in CS502 Assignment No. 01 Solution and Discussion:
Question No 01: (Marks: 10)
You are required to design (write) a simple algorithm (Only Pseudo code) which can identify a number to be Prime or Not Prime.Solution:
Question No. 01: The algorithm for the identification of Prime number is as follows,1 PRIME (int Number)
2 int Count ← 0
3 for i ← 2 to Number – 1
4 if ( Number % i equal to 0)
5 Increment Count
6 If (Count is equal to 0)
7 Number is Prime
8 else
9 Number is NOT Prime -
@zareen said in CS502 Assignment No. 01 Solution and Discussion:
Question No 02: (Marks: 10)
You are required to calculate (Step by Step) the worst case time complexity T(n) of the algorithm designed in Question No. 01.Solution:
Question No. 02: The step by stem analysis of the algorithm designed in question 1 is as follow,The time taken by each statement (step) is given as follows,
Step 1: C1 // Execute only 1 time or Constant Time or O (1)
Step 2: C2 // Execute only 1 time or Constant Time or O (1)
Step 3: n -2 // Execute n -2 times
Step 4: n -2 // Execute n -2 times
Step 5: n – 2 // Execute n -2 times
Step 6: C3 // Execute only 1 time or Constant Time or O (1)
Step 7: C4 // Execute only 1 time or Constant Time or O (1)
Step 8: C5 // Execute only 1 time or Constant Time or O (1)
Step 9: C6 // Execute only 1 time or Constant Time or O (1)Total time T(n) can be calculated as follows,
T(n) = C1 + C2 + (n -2 ) + (n -2 ) + (n -2 ) + C3 + C4 + C5 + C6
T(n) = C1 + C2 + n -2 + n -2 + n -2 + C3 + C4 + C5 + C6
T(n) = C1 + C2 + n + n + n - 6 + C3 + C4 + C5 + C6
T(n) = 3n + C1 + C2 + C3 + C4 + C5 + C6 -6
T(n) = 3n + (C1 + C2 + C3 + C4 + C5 + C6 -6)
T(n) = 3n + C7 // C7 = (C1 + C2 + C3 + C4 + C5 + C6 -6)
T(n) = n // Ignoring constant termsOr T(n) = O (n )